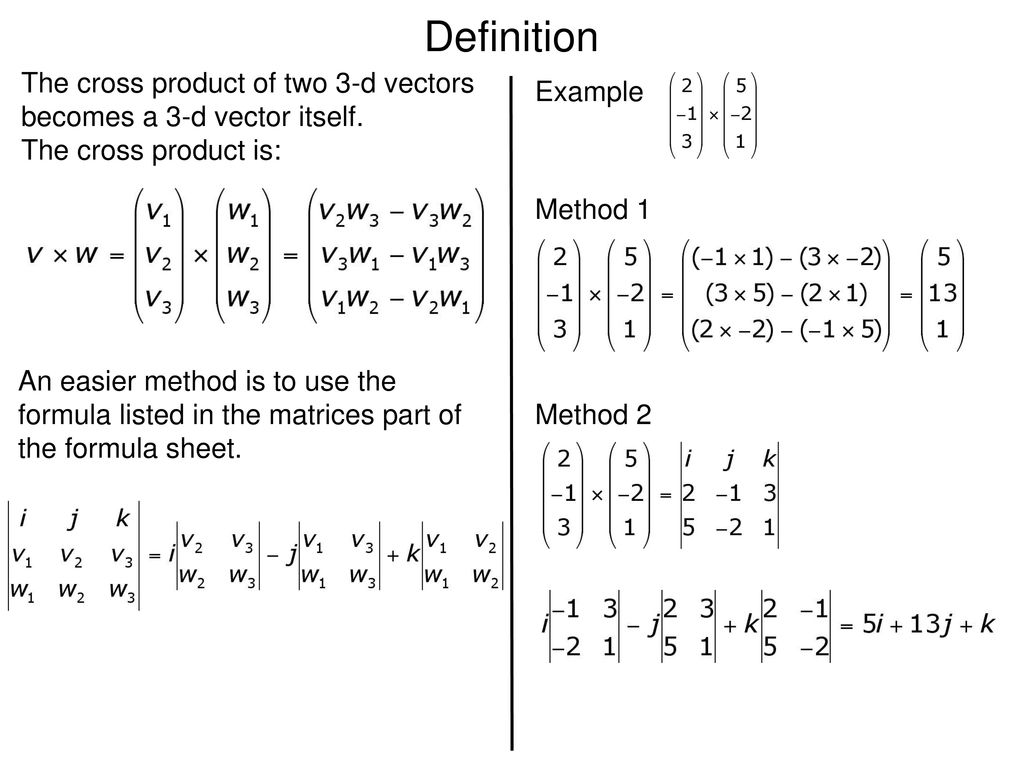
Vector Formula Sheet - Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. Vectors can be moved around as long as their length (magnitude) and. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications.
Vectors can be moved around as long as their length (magnitude) and. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column.
Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. Vectors can be moved around as long as their length (magnitude) and. Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications.
Vector Formula at Collection of Vector Formula free
Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. Vectors can be moved around as long as their length (magnitude) and. D dt t n = nt n 1 and tn dt = 1 n.
Vector Formula Sheet at Collection of Vector Formula
Vectors can be moved around as long as their length (magnitude) and. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Matrix vector = 1 a matrix with only one (1) row.
Vector Formula Sheet at Collection of Vector Formula
A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Matrix vector = 1 a matrix.
Vector Formula Sheet at Collection of Vector Formula
Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Vectors can be moved around as long as their length (magnitude) and. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Matrix vector = 1 a matrix with only one (1) row.
Vector Formula Sheet at Collection of Vector Formula
Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Vectors can be moved around as long as their length (magnitude) and. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product,.
Vector Formula Sheet at Collection of Vector Formula
Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Vectors can be moved around as long as their length (magnitude) and. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross.
Vector Formula Sheet at Collection of Vector Formula
Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. Vectors can be moved around as long as their.
Vector Formula Physics at Collection of Vector
Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. Matrix vector = 1 a matrix.
Vector Formula at Collection of Vector Formula free
Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Matrix vector = 1 a matrix.
Vector Formula Sheet at Collection of Vector Formula
Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: A comprehensive guide to vectors in r3,.
Vectors Can Be Moved Around As Long As Their Length (Magnitude) And.
D dt t n = nt n 1 and tn dt = 1 n +1 t n +1 circumference: Matrix vector = 1 a matrix with only one (1) row or 1 matrix or column. A comprehensive guide to vectors in r3, including definitions, operations, magnitudes, dot product, cross product, and applications. Ax 2+ bx + c = 0, x = b p b 4ac =(2 a ) derivatives, integrals: